Zadání

Problém vážené splnitelnosti booleovské formule

Je dána booleovská formule F proměnnných X=(x₁, x₂, ... , x_n) v konjunktivní normální formě (tj. součin součtů). Dále jsou dány celočíselné kladné váhy W=(w₁, w₂, ... , w_n).  Najděte ohodnocení Y=(y₁, y₂, ... , y_n) proměnných x₁, x₂, ... , x_n tak, aby F(Y)=1 a součet vah proměnných, které jsou ohodnoceny jedničkou,  byl maximální.

Pokyny k řešení

Problém řešte některou z pokročilých lokálních heuristik (simulované ochlazování, genetické algoritmy, tabu prohledávání).  Řešení jinými metodami prosím zkonzultovat se cvičícím nebo přednášejícím. Volby konkrétních parametrů heuristiky a jejích detailů (operace nad stavovým prostorem, kritérium ukončení, atd. atd.) proveďte sami, tyto volby pokud možno zdůvodněte a ověřte experimentálním vyhodnocením.

Hodnocení

Řešení této úlohy se obhajuje u zkoušky. Hodnotí se především postup při aplikaci heuristiky, tj. postup a experimenty, jakým jste dospěli k výsledné podobě (parametry, konkrétní operátory apod.). Například, pokud máte v řešení nějaké hodně neortodoxní prvky a pokud máte jejich výhodnost experimentálně doloženou, těžko mohou vzniknout námitky. Méně významné jsou konkrétní dosažené výsledky. Nežádáme rozhodně, aby semestrální práce měla úroveň světové výzvy Centra diskrétní matematiky Rutgersovy univerzity.

Zadání domácí úlohy

Navrhněte a implementujte program řešící problém SAT pomocí simulovaného ochlazování. Popište způsob nastavení konfiguračních parametrů algoritmu.

Řešení:

Obecné implementační poznámky:

Abych mohl vidět výsledky již při výpočtu, rozhodl jsem se vytvořit vlastní výpočetní vlákno, které se stará o výpočet, a zobrazovací třídu, která se stará o vykreslení jednoduchého grafu. Vlákno je spojeno se zobrazovací třídou pomocí několika seznamů, které uchovávají celou historii výpočtu.

Dále jsem provedl jemnou úpravu výpočetního cyklu. Musím totiž přijmout i ty stavy, které nejsou řešením. Proto jsem vedle podmínky state.better() umístil i podmínku state.isSolution(). Tím jsem trochu oddělil hledání cenově nejlepšího řešení od zjišťování a ukládání přípustných řešení.

Při psaní jsen narazil na problém, jak přinutit algoritmus, aby směřoval k řešení a ne jen k výhodné vážené funkci. Nastavil jsem proto cenovou funkci takto:
f(x) = 100.0*(0.6*(w/W) + e^(c/C))
kde:

• w - celková váha formule
• W - maximální váha formule (všechny proměnné na true)
• c - počet splněných klausulí
• C - maximální počet splněných klausulí
• Hodnota f(x) je v intervalu <0.0;100*(e+0.6)>. Funkci exp() jsem si vybral proto, že její hodnota roste s přibývajícím argumentem více než lineárně. Chtěl jsem použít větší tlak při lepší splnitelnosti formule.Ohodnocení je tedy čím větší, tím lepší.

Hodnota konstanty u váhy je zjištěná experimentálně. Pokud ji použiji vyšší, než 0.6, program obtížně nalezá přípustný stav. Pokud ji dám menší, než 0.6 (např. 0.3) nalezám první přípustný stav poměrně brzo a celkový počet nalezených přípustných stavů je také cca 3x větší.

Uvnitř algoritmu

tryState(x): Provedu negaci jedné proměnné, kterou vyberu náhodně. Zkoušel jsem i v závislosti na teplotě (a tudíž i na procentu přijatých stavů) měnit počet změněných bitů. Nepřineslo to žádné zlepšení.

equilibrium(): pevně stanovený počet iterací. Pomalu roste s chládnutím.
cool(): klesá s koeficientem α geometrickou řadou.
souvislost těchto dvou funkcí: použil jsem buď rychlé chládnutí a velký počet iterací, nebo pomalé chládnutí a menší počet iterací. Přišlo mi, že na výsledek to nemá skoro vliv, kterou variantu použiji.

frozen(): okamžik, kdy klesne počet přijatých stavů pod určitou úroveň.

Příklady průběhů výpočtu:

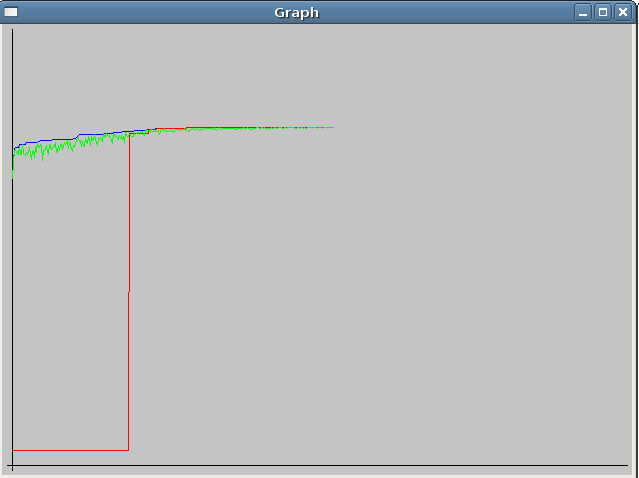
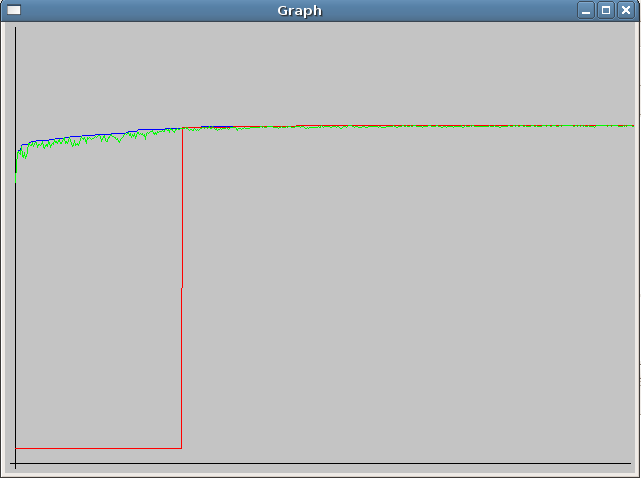
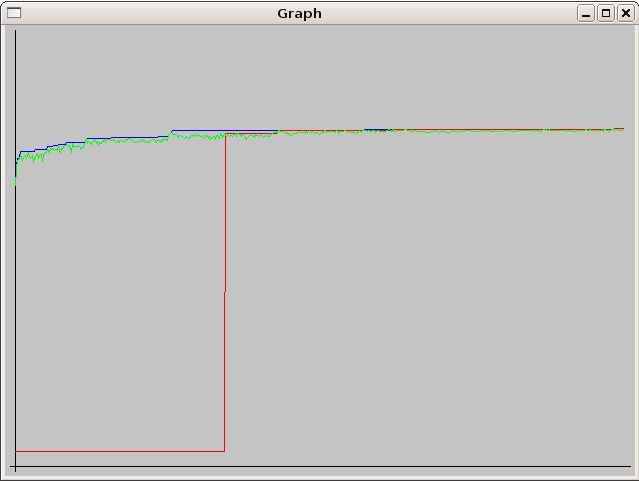
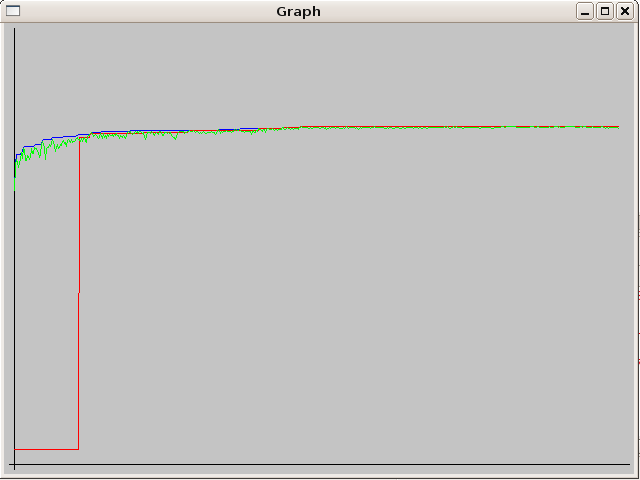
Zde jsem přidal pár screenshotů průběhu výpočtu. Grafy jsou bez označení os. Na x-ové ose je vždy čas a na y-ové ose je hodnota f(x). Y-nové hodnoty jsou všechny tři ve stejném měřítku. Hodnoty jsem do os nevykresloval, protože výsledek se mi zobrazuje v programu a zde mne zajímal pouze průběh.

Popis jednotlivých barev v grafech:

• zelená - aktuální stav
• modrá - nejlepší nalezený i nepřipustný stav
• červená - nejlepší nalezený přípustný stav

Závěr

Takto nastavený algoritmus konverguje. Ověřeno experimentálně.

Co by se dalo na programu vylepšit/vyzkoušet, jsou tyto části: implemetnace metody equilibrium() tak, aby používala nejaký způsob zpětné vazby, zkusit změnit chladicí křivku, nebo dodělat nakonec iterativní deterministickou heuristiku, která po skončení tohoto algoritmu provede přechod až do lokálního maxima (pokud v něm ještě nebudeme).

Program je psán v Javě verze 5.0. Stáhnout si ho můžete zde, nebo se můžete podívat do zdrojových kódů.