Úloha do předmětu 36PAA 2005/2006

Řešení problému batohu

Karel Podvolecký

5. ročník, obor počítače, K336 FEL CVUT, Karlovo nám. 13, 121 35 Praha 2

March 13, 2006

Zadání

Je dáno

celé číslo n (počet věcí)
celé číslo M (kapacita batohu)
konečná množina V={v₁, v₂, ... ,v_n } (hmotnosti věcí)
konečná množina C={c₁, c₂, ... ,c_n } (ceny věcí)

0/1 problém batohu

Nejznámější varianta je optimalizační. Pokud se mluví o "problému batohu" bez bližšího určení, většinou se rozumí tato verze.

Zkonstruujte množinu X={x1, x2, ... ,xn }, kde každé xi je 0 nebo 1, tak, aby

platilo
v₁x₁+v₂x₂+ ... + v_nx_n <= M
(batoh nebyl přetížen)
výraz
c₁x₁+c₂x₂+ ... + c_nx_n
nabýval maximální hodnoty pro všechny takové množiny (cena věcí v batohu byla maximální).

Řešení:

Pro metodu hrubé síly jsem použil reprezentaci stavového prostoru stromem. Výpočet probíhal průchodem do hloubky. Abych zamezil zbytečnému testování stavů, které jsem již prošel, seřadil jsem si předměty podle nějakého kritéria (nezáleží podlejakého) a přidával jsem do batohu pouze následující předměty.

Pro metodu heuristickou jsem použil jednoduchou ohodnocovací funkcí h=c/w, kde c je cena předmětu a w je jeho váha. Takto ohodnocené předměty se setřídí podle koeficientů a vkládají se do batohu dokud je tam místo.

Tabulka naměřených hodnot:

Typ algoritmu	Celkový počet věcí	4	10	15	20	22
Typ algoritmu	Veličina	4	10	15	20	22
Hrubá síla	čas [ms]	0	1	59	2330	9598
Heuristika	Δ_ø[%]	7.2	2.9	0.8	1.3	1.4
Heuristika	Δ_max.[%]	68.4	15.8	5.6	6.1	8.8

Výsledné grafy:

Čas výpočtu

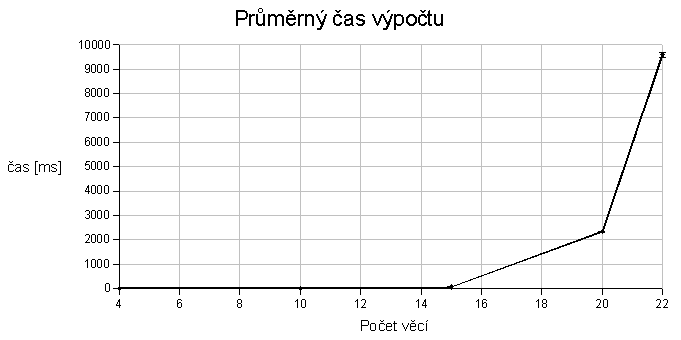
časy výpočtu

Je vidět, že daný průběh se velmi podobá exponenciální funkci. Časová složitost roste velmi strmě.

Odchylky heuristiky od optimálního řešení

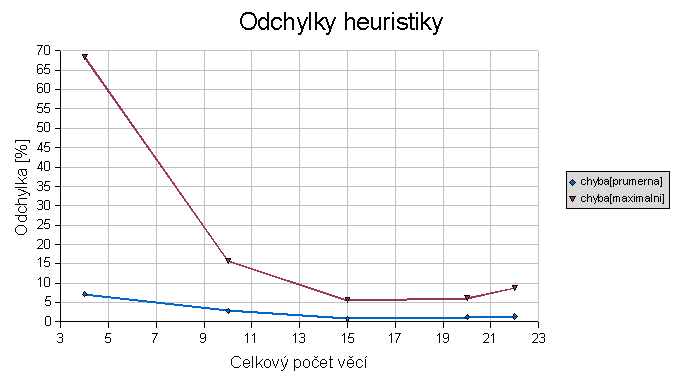
odchylky heuristiky

Odchylku od optimálního řešení jsem spočítal podle vzorce Δ=|c - c_opt|/c_opt*100.
Z grafu je jasně vidět, že odchylky klesají s rostoucím počtem věcí. Je to dáno hlavně tím, že s rostoucím počtem věcí se v testovaném vzorku konfigurací problému zjemňují vztahy mezi jednotlivými věcmi. Vzniká tak menší rozdíl mezi optimální cenou a cenou heuristiky.

Závěr

V závěru bych si povšimnul jedné zajímavé vlastnosti použité heuristiky. Jak je vidět na grafech výše, maximální a průměrná odchylka se s rostoucím počtem věcí přibližují. To znamená, že nám tato heuristika dává celkem dobré výsledky v řádově lepším čase.

Program je psán v Javě verze 5.0. Stáhnout si ho můžete zde, nebo se můžete podívat do zdrojových kódů.

<<zpět