Úloha do předmětu 36PAA 2005/2006
Řešení problému batohu
Karel Podvolecký
5. ročník, obor počítače, K336 FEL CVUT, Karlovo nám. 13, 121 35 Praha 2
March 13, 2006
Zadání:
Metoda větví a hranic
Naprogramujte řešení 0/1 problému batohu metodou větví a hranic, kde omezujícím faktorem je hodnota optimalizačního kritéria:
Cact + Crest < Cbest
Kde:
- Cact - je cena v aktuálním stavu
- Crest - je cena celé podvětvi
- Cbest - je cena nejlepšího řešení
Pokud podmínka platí, potom ořízneme celou podvětev, protože v ní nemůžeme nalézt lepši řešení.
Dynamické programování
0/1 problém batohu
Existují nejméně dvě dekompozice. Z prvé uvedené se odvozuje plně polynomiální aproximační schéma pro problém batohu, má tedy i teoretický význam.
Podle celkové ceny. Označme E(i,c) instanci 0/1 inverzního problému batohu se zadanou cenou c, která vznikne z řešené instance omezením na prvých i věcí. Označme dále W(i,c) sumární hmotnost věcí řešené instance. Pak platí
- W(0,0)=0
- W(0,c) = nekonečno pro všechna c>0
- W(i+1,c) = min (W(i,c), W(i,c-ci+1)+wi+1) pro všechna i>1.
Z výsledných řešení W(n,c) vybereme řešení, pro které je W(n,c) > M pro největší c. Je zřejmé, že řešení můžeme omezit na c menší nebo rovné součtu cen všech věcí.
Výše uvedená závislost je pro dynamické programování charakteristická. Postup řešení lze formulovat buď rekurzí (řešit problémy E(n,c) pro všechna c a rekurzivně potřebné podproblémy) nebo dopředně - začít s E(0,c) pro všechna c a generovat všechna možná řešení problémů E(i,c) pro i = 1, ... ,n. Je třeba zabránit tomu, aby byl jeden a týž problém řešen opakovaně, jinak se ztrácejí přednosti metody.
Kombinovaná heuristika
Problém vyřešte heuristikou podle poměru cena/hmotnost. Výsledné řešení porovnejte s řešením, které se skládá pouze z jediné nejcennější věci.
Řešení:
Metoda větví a hranic
Pro metodu větví a hranic jsem vytvořil druhou tabulku, která vlastně představuje suffixový součet cen všech předmětů. Použil jsem původní algoritmus pro hrubou sílu, který jsem rozšířil právě o test nad tabulkou suffixového součtu, podle optimalizačního kritéria.
Metoda dynamického programování
U metody dynamického programování jsem použil upravenou reprezentaci dat. Nesestrojoval jsem celou tabulku, ale pouze 2 relevantní sloupečky. Výpočet pak probiha tak, že se z předchozího sloupečku počítají hodnoty nového. Pak se sloupečky prohodí a výpočet se opakuje. Abych si tohle ale mohl dovolit, musím si udržovat u každého stavu cestu, kterou jsem se do něj dostal. Takze po skončení výpočtu se najde řádek s největší váhou, ale který zároveň unese batoh a podle odkazů se zrekonstruují vložené předměty. Pro jednoduchost do jednotlivých uzlů mimo odkazu na předchozí uzel ukládám i odkaz na daný předmět, pokud je vložený.
Metoda kombinovaná heuristiky
Tato metoda je jednoduchá. Prostě se pustí na danou instanci problému jednak heuristika c/w a potom heuristika nejcennější věci a jako výsledek se prohlásí lepší řešení.
Tabulka naměřených časů:
| Celkový počet věcí | 4 | 10 | 15 | 20 | 22 | 25 | 27 | 30 | 32 | 35 | 37 | 40 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Algoritmus | ||||||||||||
| Větve a hranice | 0,11 | 1,5 | 0,5 | 6,25 | 26,27 | 40 | 67,15 | 236,97 | 635,25 | 1166,97 | 970,86 | 11812,9 |
| Dynamické programování | 0,83 | 4,7 | 4,13 | 5,45 | 6,36 | 8,12 | 9,26 | 10,93 | 11,22 | 16,06 | 16,03 | 18,75 |
| Kombinovaná heuristika | 0,3 | 1,6 | 0,36 | 0,1 | 0,32 | 0,6 | 0,59 | 0,5 | 0,5 | 0,07 | 0,43 | 0,29 |
Pozn: Tabulka ukazuje průměrné časy pro jednotlivé počty věcí. Časy jsou v milisekundách.
Tabulka počtů navštívených stavů:
| Celkový počet věcí | 4 | 10 | 15 | 20 | 22 | 25 | 27 | 30 | 32 | 35 | 37 | 40 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Algoritmus | ||||||||||||
| Větve a hranice | 122 | 556 | 370 | 5216 | 20489 | 29232 | 45525 | 147182 | 370865 | 618669 | 488797 | 5801199 |
| Dynamické programování | 25295 | 67633 | 93961 | 126648 | 139588 | 162869 | 171371 | 196813 | 202147 | 222995 | 228805 | 254079 |
| Kombinovaná heuristika | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Pozn: U metody dynamického programování znamená navštívený stav
něco trochu jiného, proto se i časy liší od metody větví a hranic.
Počty stavů jsou zprůměrované pro jednotlivé počty věcí.
Výsledné grafy:
Čas výpočtu
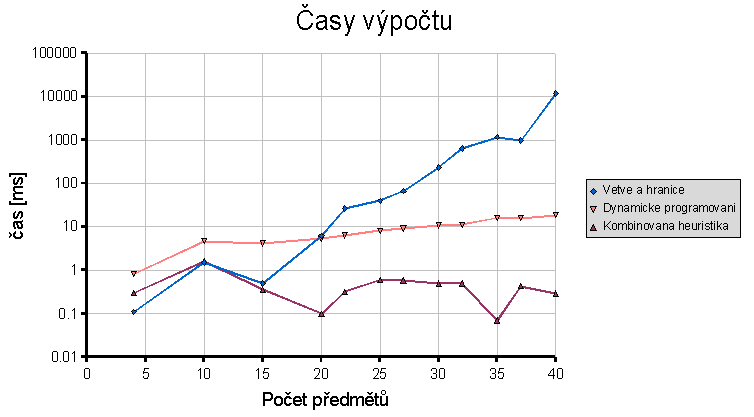
Aby zde bylo co nejlépe možno porovnat výpočetní časy, musel jsem zobrazit časovou osu v logaritmickém měřítku. Jsou zde lépe vidět strmosti, s jakými roste výpočetní čas.
Průměrné zrychlení výpočtu
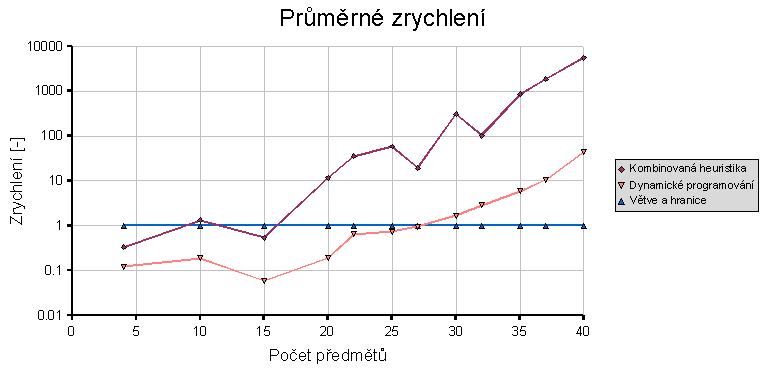
Zrychlení jsem zde vztáhnul k metodě větví a hranic. Proto je zrychlení této metody rovno 1.
Průměrná odchylka řešení
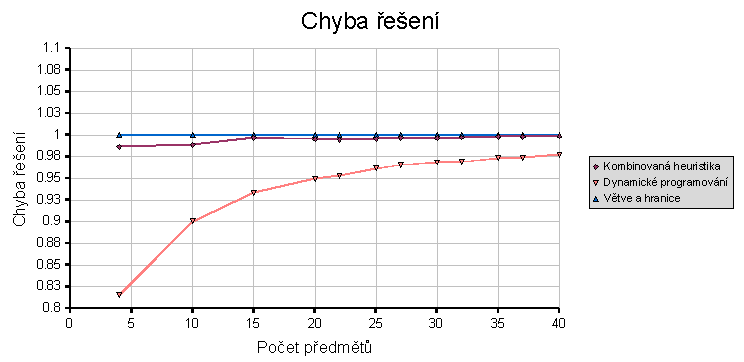
Protože metoda větví a hranic dává optimální řešení problému, vztahoval jsem odchylky k ní. Proto má ve všech konfiguracích hodnotu 1.
Závěr
Metoda větví a hranic dává optimální řešení. Ve výsledku je rychlejší než metoda hrubé síly, nicméně podle jemného zvlnění tvaru časové křivky bych odhadoval, že bude datově závislá. To lze odvodit i z principu průchodu stavového prostoru. Pokud bude řešení nalezeno už na začátku, bude spousta velkých podstromů ořezána.
U metody dynamického programování je největší počet navštívených stavů. Protože se s nimi ale pracuje jinak, než u metody větví a hranic. Stále je z časového hlediska výhodnější. Pokud bychom chtěli srovnávat i paměťovou náročnost, bylo by to složitější. Museli bychom "spočítat" všechny instance uzlů, protože v algoritmu je použita optimalizace popsaná výše. Takže celková paměťová náročnost je závislá jak na maximální ceně, tak na konkrétních datech, tj. kolik bude prázdných míst v tabulce.
Co mě ale překvapilo, byla kombinovaná heuristika. A to hned dvakrát. Za prvé jsem zjistil, že výsledky z heuristiky nejcennější věci se použili ze všech asi 500 výpočtů jen asi 5x. A za druhé, že odchylka od optimálního řešení je dokonce nižší, než u dynamického programování. Navíc čas výpočtu je podle grafu nezávislý na počtu věcí, což je pro nás dobrá zpráva. Také z tabulky je vidět, že tato heuristika defakto nenavštívila zádný stav, protože se předměty vlastně projdou 2x. Je ale pravda, že je potřeba je seřadit, takže celkovou asymptotickou složitost tohoto algoritmu zřejmě tvoří pouze složka řazeni : O(n*logn).
Program je psán v Javě verze 5.0. Stáhnout si ho můžete zde, nebo se můžete podívat do zdrojových kódů. Detailní výsledky naleznete v archívu.