Úloha do předmětu 36PAA 2005/2006
Řešení problému batohu
Karel Podvolecký
5. ročník, obor počítače, K336 FEL CVUT, Karlovo nám. 13, 121 35 Praha 2
April 25, 2006
Zadání:
Porovnejte metody Větví a hranic, c/w heuristiku a dynamické programování z hlediska měnících se parametrů zadaných při generování zadání.
Parametry:
- n - celkový počet věcí v zadání
- max ci - maximální cena jedné věci
- max wi - maximální váha jedné věci
- M/∑(wi) - kolikrát je kapacita batohu větší než součet vah všech věcí
- granularita vah - určuje jestli se generovaly spíše lehčí věci, nebo spíše těžší věci
Řešení:
Testování jednotlivých metod jsem prováděl pomocí webového generátoru zadání. Ten má k dispozici 6 parametrů, jak ovlivnit generované zadání. Testoval jsem závislost jednotlivých metod právě na nastavení těchto parametrů. Jako střední nastavení jsem zvolil toto:
- n = 25
- max ci = 250
- max wi = 100
- M/∑(wi) = 0.6
- granularita = nerozliš.
- exponent = 1.0
Počet instancí každého problému jsem zvolil 50. Výsledky jsou vždy zprůměrované.
U metod větví a hranic a dynamického programování jsem sledoval parametr počet navštívených stavů, u metody c/w heuristiky jsem sledoval průměrnou odchylku od optimálního řešení.
Počet testovaných věcí
Měnil jsem počet věcí v konfiguraci od 20 do 30.
Tabulka závislosti počtu věcí:
| Algoritmus | Branch And Bounds | Dynamic Programming | c/w Heuristic |
|---|---|---|---|
| n | |||
| 20 | 18446 | 123109 | 0.6 |
| 22 | 30439 | 136958 | 0,39 |
| 25 | 65950 | 157025 | 0,48 |
| 27 | 213839 | 170509 | 0,19 |
| 30 | 724085 | 186743 | 0,51 |
Grafy:
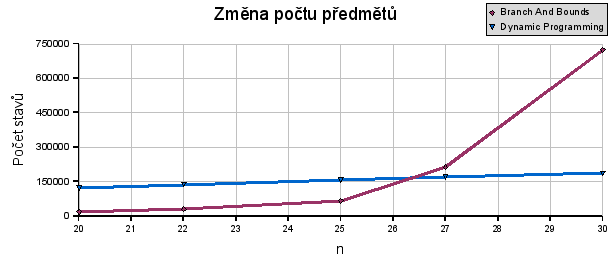
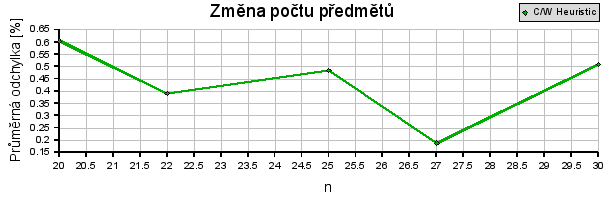
Zde se projevila jemná závislost dynamického programování na počtu věcí. Ta se dá jednoduše zdůvodnit tím, že při rostoucím počtu věcí se zvětšuje i počet řádek v tabulce a tím roste i počet navštívených stavů.
Pro metodu větví a hranic je závislost jasně vidět. Čím více věcí je v konfiguraci, tím více roste počet navštívených stavů.
U c/w heuristiky by se měla chyba snižovat, nicméně poslední hodnota tomu neodpovídá. Bylo by potřeba provést testy i pro větší počty věcí.
Maximální cena jedné věci
Měnil jsem maximální cenu jedné věci v generátoru od 200 do 300.
Tabulka závislosti maximální ceny jedné věci:
| Algoritmus | Branch And Bounds | Dynamic Programming | c/w Heuristic |
|---|---|---|---|
| max ci | |||
| 200 | 120748 | 124695 | 0.5 |
| 225 | 70985 | 141984 | 0.29 |
| 250 | 135691 | 157556 | 0.47 |
| 275 | 99120 | 169277 | 0.23 |
| 300 | 102151 | 188997 | 0.45 |
Grafy:
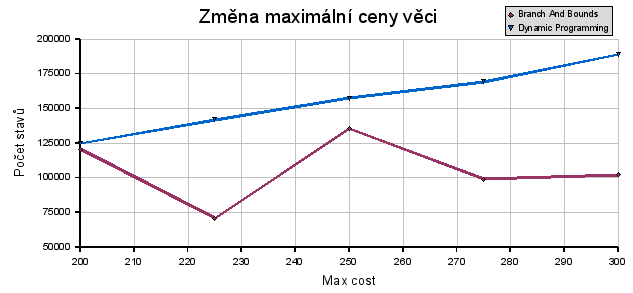
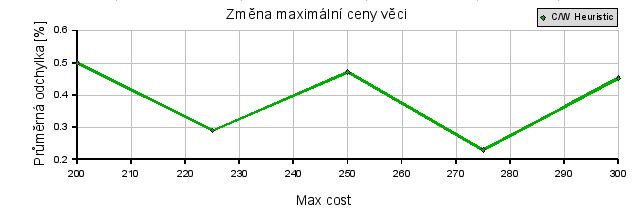
Jediná jasná závislost na maximální ceně se projevila u dynamického programování, což odpovídá předpokladům.
Poměr kapacity batohu a celkové hmotnosti věcí v konfiguraci
Tento parametr znamená, o kolik bude převyšovat váha všech věcí nad kapacitou batohu. Jinými slovy, kolik věcí se průměrně vleze do batohu.
Tabulka M/∑wi:
| Algoritmus | Branch And Bounds | Dynamic Programming | c/w Heuristic |
|---|---|---|---|
| M/∑wi | |||
| 0,2 | 433024 | 159011 | 1,02 |
| 0,4 | 807688 | 156392 | 0,57 |
| 0,6 | 102340 | 157249 | 0,29 |
| 0,8 | 2033 | 153924 | 0,35 |
| 1.0 | 98 | 159992 | 0.0 |
Grafy:
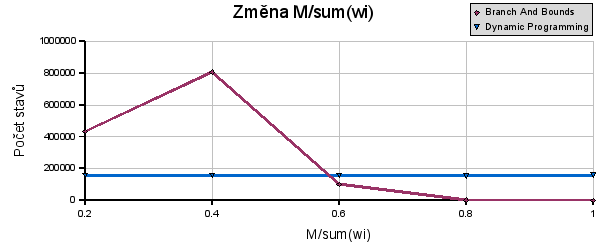
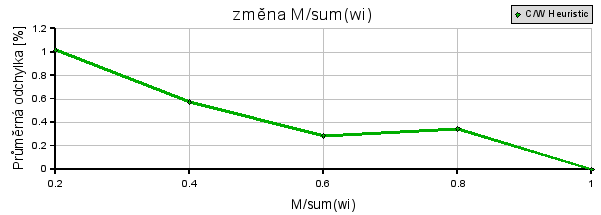
Zde průběhy odpovídají předpokladům. Dynamické programování není citlivé na tento parametr, protože je závislé pouze na celkové ceně a počtu předmětů. Oproti tomu jak heuristika, tak metoda větví a hranic s rostoucím koeficientem jsou efektivnější. Je to způsobeno tím, že najdou řešení hned na první průchod, protože do batohu nahází všechny věci, označí to jako nejlepší řešení a zbytek procházení už defakto zahodí.
Maximální váha jednoho předmětu
Maximální váhu jsem testoval v rozsahu od 50 do 150. Předpokladal bych minimální vliv na testované metody. Maximálně u c/w heuristiky by mohlo dojít ke zhoršení výsledků z důvodu větších odstupů výsledných cen.
Tabulka závislosti maximální váhy jednoho předmětu:
| Algoritmus | Branch And Bounds | Dynamic Programming | c/w Heuristic |
|---|---|---|---|
| max wi | |||
| 50 | 115302 | 154644 | 0,3 |
| 75 | 92463 | 156684 | 0,49 |
| 100 | 116628 | 150100 | 0,4 |
| 125 | 106796 | 162228 | 0,35 |
| 150 | 113815 | 157329 | 0,59 |
Grafy:
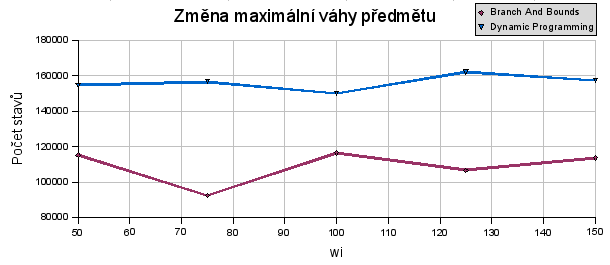
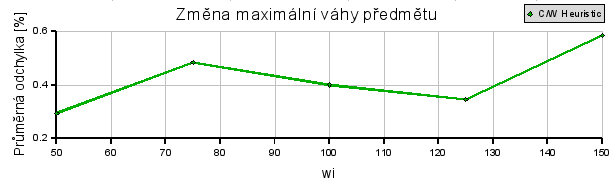
Pro metody dynamického programování a větví a hranic jsou výsledky podle očekávání. Dané zvlnění grafů je dané výběrem testovaných dat.
U c/w heuristiky je tendence v tomto grafu nerozhodnutelná. Nicméně subjektivně odchylka roste. Lepších závěrů a potvrzení/vyvrácení předpokladu bych dosáhl při rozšíření hodnot testovaného parametru.
Změny granularity a exponentu
Protože granularita a exponent jsou svázané veličiny, musel jsem testování provés v závislosti techto dvou paramterů. Z tohoto důvodu jsem se omezil na velmi malou množinu testovaných hodnot, a proto jsem nedělal ani grafy.
Tabulka změn granularity:
| Algoritmus | Branch And Bounds | Dynamic Programming | c/w Heuristic | |
|---|---|---|---|---|
| Granularita | Exponent | |||
| Malá | 0,5 | 116126 | 155211 | 0,67 |
| 1,5 | 13890 | 157157 | 0,52 | |
| Velká | 0,5 | 106301 | 154479 | 0,3 |
| 1,5 | 239668 | 155477 | 0.21 | |
| Nerozlišuje | 0,5 | 94887 | 156586 | 0.38 |
| 1,5 | 79439 | 150546 | 0.51 | |
Pokud se blíže podíváme do výsledné tabulky, uvidíme i přesto jisté závislosti. Metoda dynamického programování je očividně nezávislá na nastavení těchto parametrů. C/W heuristika se motá okolo stejných hodnot, takže není možné rozhodnout o nějaké závislosti. Oproti tomu metoda větví a hranic je na nastavení těchto parametrů velmi závislá. Skok počtu navštívených stavů se pohybuje při upřednostňování jednoho druhu věcí od 2 do 10. Pokud v batohu budou věci pomíchaných velikostí, je to již skoro nezajímavé.
Závěr
Jak již bylo zmíněno u každého testovaného parametru, některá měření by chtělo rozšířit, aby se potvrdily případné závislosti, jinde to bylo vidět hned. Ve výsledku se ale potvrdily výsledky, které jsem očekával od jednotlivých metod řešení.
Program je psán v Javě verze 5.0. Stáhnout si ho můžete zde, nebo se můžete podívat do zdrojových kódů. Zdroj grafů v ods nebo pdf formátu.