Úloha do předmětu 36PAA 2005/2006
Řešení zobecněného problému kýblů
Karel Podvolecký
5. ročník, obor počítače, K336 FEL CVUT, Karlovo nám. 13, 121 35 Praha 2
April 4, 2006
Zadání
Problém kýblu
Základní problém je definován takto: K dispozici jsou dva kýble (předem daných obecně rozdílných objemů), vodovodní kohoutek a kanál. Na počátku jsou oba kýble prázdné. Vaším úkolem je docílit toho, aby v jednom kýblu byla voda o předem stanoveném objemu, přičemž můžete pouze naplnit plný kýbl z kohoutku, vylít celý kýbl do kanálu a přelít jeden kýbl do druhého tak, aby druhý kýbl nepřetekl.
Problém lze zobecnit tím, že připustíme užití většího počtu kýblů, aby na počátku řešení byla v kýblech nějaká voda, a že předepíšeme koncový objem vody v každém kýblu.
Zadání domácí úlohy
Navrhněte a implementujte heuristiku řešící zobecněný problém dvou kýblů. Heuristiku otestujte na následujících příkladech a srovnejte s prohledáváním stavového prostoru do šířky (BFS).
Konfigurace kýblů:
Konfigurace 1
| Kýble (objem) | 14 | 10 | 6 | 2 | 8 |
|---|---|---|---|---|---|
| Počátek | 0 | 0 | 1 | 0 | 0 |
| Stav 1 | 12 | 6 | 4 | 1 | 8 |
| Stav 2 | 14 | 4 | 5 | 0 | 4 |
| Stav 3 | 12 | 6 | 6 | 2 | 4 |
| Stav 4 | 0 | 2 | 1 | 2 | 8 |
Konfigurace 2
| Kýble (objem) | 15 | 12 | 8 | 4 | 6 |
|---|---|---|---|---|---|
| Počátek | 0 | 0 | 0 | 0 | 0 |
| Stav 1 | 5 | 5 | 5 | 0 | 1 |
| Stav 2 | 12 | 1 | 3 | 4 | 5 |
| Stav 3 | 11 | 1 | 3 | 4 | 5 |
| Stav 4 | 3 | 12 | 4 | 0 | 6 |
| Stav 5 | 2 | 0 | 4 | 3 | 6 |
Konfigurace 3
| Kýble (objem) | 14 | 10 | 12 | 3 | 8 |
|---|---|---|---|---|---|
| Počátek | 0 | 0 | 0 | 0 | 0 |
| Stav 1 | 13 | 9 | 12 | 2 | 7 |
| Stav 2 | 1 | 5 | 5 | 3 | 4 |
| Stav 3 | 0 | 9 | 6 | 3 | 1 |
| Stav 4 | 12 | 0 | 12 | 0 | 2 |
| Stav 5 | 7 | 3 | 7 | 0 | 0 |
| Stav 6 | 7 | 0 | 7 | 0 | 7 |
Řešení:
Obecné implementační poznámky:
Problém je implementován pomocí statického pole reprezentujícího celý stavový prostor. Protože je úloha specifikována jen na pevně zadaný počet kýblů, dá se to tímto způsobem zjednodušit a i výrazně zrychlit. Každý uzel stavového prostoru odkazuje na svého předka a dále obsahuje pár dalších více či méně neužitečných atributů. Jedna (ne)výhoda Javy je, že po vytvoření statického pole objektů, se musí každý prvek pole ručně vytvořit. Toho se zde dá efektivně využít, takže se jednotlivé uzly stavového prostoru alokují až při průchodu. Tím se automaticky šetří jak paměť, tak čas oproti jednorázové inicializaci celého stavového prostoru.
Hrubá síla
Pro hrubou sílu jsem použil algoritmus prohledávání do šířky: BFS. Je použit modifikovaný spojový seznam jako fronta uzlů. Tento seznam si pamatuje počty vložení a vyjmutí.
Heuristika
Jako heuristiku (pracovně nazvanou Delta Heuristic) jsem použil jako ohodnocovací funkci součet delta vzdáleností každého kýble.
Tj. h=∑|siact - siend|
Kde s - je stav naplnění kýble (act - aktuální, end - koncový).
U heuristiky je použita prioritní fronta, která řadí právě podle tohoto ohodnocení.
Tabulka naměřených hodnot:
| Konfigurace | BFS | Heuristika | |||||
|---|---|---|---|---|---|---|---|
| délka cesty | navštívených stavů | vygenerovaných stavů | délka cesty | navštívených stavů | vygenerovaných stavů | ||
| Konfigurace 1 | Stav 1 | 10 | 8954 | 8992 | 20 | 78 | 734 |
| Stav 2 | 8 | 5948 | 8055 | 21 | 545 | 1758 | |
| Stav 3 | 8 | 5963 | 8064 | 8 | 12 | 120 | |
| Stav 4 | 3 | 28 | 182 | 4 | 6 | 55 | |
| Konfigurace 2 | Stav 1 | 16 | 49257 | 49350 | 50 | 8055 | 27171 |
| Stav 2 | 12 | 32615 | 40021 | 40 | 9278 | 28297 | |
| Stav 3 | 11 | 22887 | 31391 | 49 | 5264 | 19081 | |
| Stav 4 | 5 | 215 | 790 | 12 | 449 | 1980 | |
| Stav 5 | 7 | 1932 | 4727 | 22 | 657 | 2611 | |
| Konfigurace 3 | Stav 1 | 14 | 59016 | 59199 | 43 | 1368 | 4349 |
| Stav 2 | 12 | 55588 | 58703 | 39 | 388 | 3927 | |
| Stav 3 | 10 | 34008 | 46306 | 39 | 811 | 5278 | |
| Stav 4 | 5 | 253 | 1009 | 12 | 52 | 468 | |
| Stav 5 | 7 | 2827 | 7461 | 10 | 119 | 1162 | |
| Stav 6 | 9 | 15746 | 27533 | 38 | 960 | 7090 | |
Výsledné grafy:
Konfigurace 1
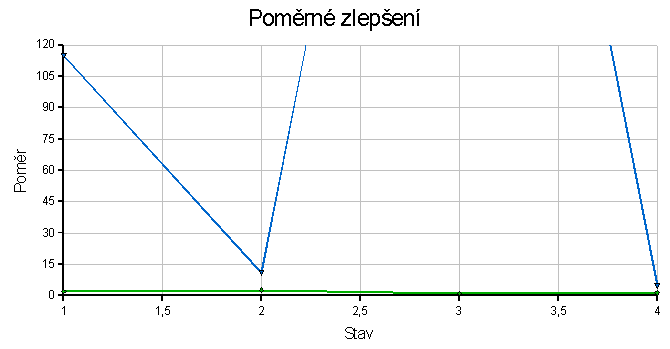
Zelená křivka ukazuje poměr délky cest heuristika/BFS - čím výš, tím je to pro heuristiku horší.
Modrá křivka zobrazuje poměr počtu navštívených stavů BFS/heuristika - čím výš, tím líp pro heuristiku
Konfigurace 2
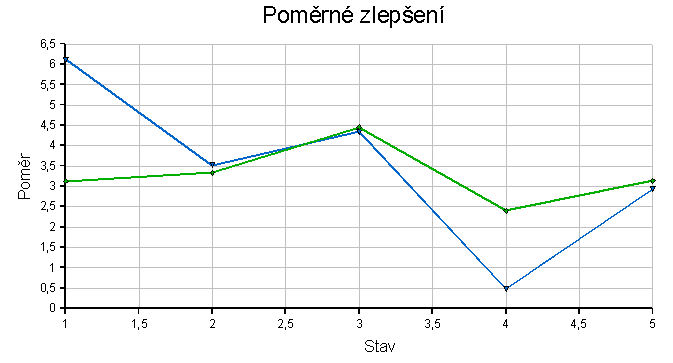
Zelená křivka ukazuje poměr délky cest heuristika/BFS - čím výš, tím je to pro heuristiku horší.
Modrá křivka zobrazuje poměr počtu navštívených stavů BFS/heuristika - čím výš, tím líp pro heuristiku
Konfigurace 3
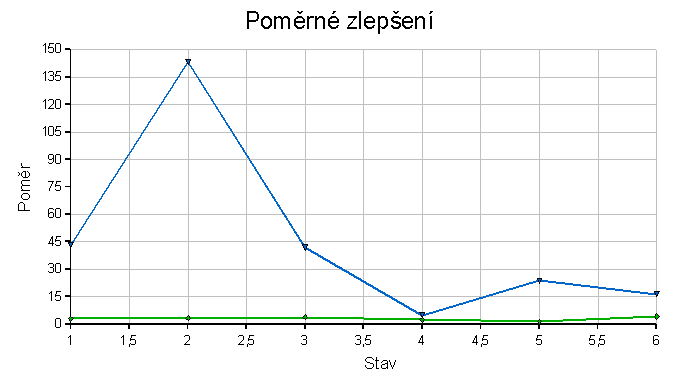
Zelená křivka ukazuje poměr délky cest heuristika/BFS - čím výš, tím je to pro heuristiku horší.
Modrá křivka zobrazuje poměr počtu navštívených stavů BFS/heuristika - čím výš, tím líp pro heuristiku
Závěr
Z grafů vidíme, že heuristika drasticky snižuje počet navštívených stavů. Také se ale zhoršují délky cest.
Nicméně nejhorší poměr byl necelých 5. Pokud ale hledáme jakékoliv řešení, pak je tato heuristika výborná.
Nicméně další věc, které je patrná z grafů, je závislost heuristiky na konkrétních datech. Když porovnáme konfigurace
1 a 3 s konfigurací 2, pak je jasně vidět, že konfigurace 2 naší heuristice moc nesedla.
Program je psán v Javě verze 5.0. Stáhnout si ho můžete zde, nebo se můžete podívat do zdrojových kódů. Zpracované výsledky si můžete prohlédnout ve stručné nebo podrobné formě.