Semestrální projekt PAR 2004/2005
Paralelní algoritmus pro řešení problému
Michal Bartoň
Karel Podvolecký
5. ročník, obor počítače, K336 FEL CVUT, Karlovo nám. 13, 121 35 Praha 2
January 3, 2006
1 Definice problému a popis sekvenčního algoritmu
Vstupní data:
- n = přirozené číslo představující celkový počet žetonů, n>3. Žeton i ma průměr i.
- s = přirozené číslo představující počet tyček, n/4>s>3
- r = číslo cílové tyčky, r ≤ s
- V[1,..,s] = množina neúplných hanoiských věží.
Data obsahuje zdrojový kód programu jako #define
Definice:
Hanoiská věž o výšce k je věž k žetonů, které jsou uspořádány od nejmenšího k největšímu a rozdíly ve velikostech sousedních žetonu jsou vždy 1. Neuplná hanoiská věž o výšce k je věž k žetonů, o průměrech d1 ≤ d2 ≤ .. ≤ dk, kde alespoň jedna nerovnost je ostrá. Například pro k=5 je to věž 2,3,7,8,10.
Generování počátečního stavu:
V pořadí průměru žetonů n,n-1,..,1 se žetony náhodně rozhazují na s tyček, takže vznikne s obecně neuplných hanoiskych věží.
Pravidla:
Jeden tah je přesun žetonu z vršku jedné věže na jedné tyčce na jinou prázdnou tyčku nebo na věž začínající žetonem s větším průměrem.
Úkol:
Na zadané tyčce r postavit úplnou hanoiskou věž pomocí minimálního počtu tahů.
Výstup algoritmu:
Výpis počtu tahů a jejich posloupnosti v následujícím formátu: hloubka,původní tyčka -> cílova tyčka. Výstup dále také obsahuje znázornění hanoiských věží.
Sekvenční algoritmus:
Sekvenční algoritmus je typu BB-DFS s neomezenou hloubkou prohledávání (obecně se mohou pro s>3 při prohledávání generovat cykly). Hloubku prohledávání musíme omezit horní mezí (viz dále). Ve stavu, kdy nelze přesunout zádny žeton, se provede návrat. Cena, kterou minimalizujeme, je počet tahů. Algoritmus končí, když je počet tahů roven dolní mezi, jinak prohledává celý stavový prostor do hloubky dané horní mezí.
Těsnou dolní mez počtu tahů lze určit takto: je-li žeton na cílové tyčce, ale není na správné pozici, pak musí provést aspon 2 tahy. Je-li žeton na jiné než cílové tyčce, pak musí provést aspoň 1 tah. Dolní mez je součet počtů tahů pro všechny žetony. Tato dolní mez je dosažitelná pro dostatečně velká s.
Těsná horní mez na počet tahů (lze odvodit řešením rekurentní rovnice): (2n/(s-2)-1)(2s-5)
Implementační odchylky od zadání:
Algoritmus vždy jako první vytvářel cykly až do maximální hloubky. Proto jsme se rozhodli cykly 1. úrovně ošetřit jednoduchou podmínkou.
Důležité je taky zmínit, že omezení na počet tyčí v závislosti na počtu žetonů vedlo na minimální zadání typu: n=17,s=4 se ukázalo v praxi neřešitelné a proto v3echna měření tyto podmínky nerespektují.
Poslední úprava spočívala v dynamické změně maximální hloubky na hloubu nejlepšího nalezeného řešení, což při troše štěstí může v určitých konfiguracích přispět k výraznému urychlení.
Tabulka naměřených hodnot sekvenčního řešení:
| Konfigurace | 1 CPU |
|---|---|
| S=5, N=6, R=4 | 181s |
| S=5, N=6, R=5 | 210s |
| S=7, N=6, R=0 | 1202s |
2 Popis paralelního algoritmu a jeho implementace v MPI
Zadání:
Paralelní algoritmus je typu G-PBB-DFS-D, hledání dárce algoritmem ACZ-AHD, dělení zásobníku pomocí R-ADZ.
Strategie průchodu a ukončování paralelního DFS (G-PBB-DFS-D)
Všechny procesory vědí nebo se dozvědí počáteční hodnotu horní i dolní meze ceny rešení. Každý procesor, který nalezne lepší řešení než jemu známé nejlepší řešení, neaktualizauje pouze svou informaci, ale rozešle zprávu typu jeden-všem ostatním procesorům, které si nastaví informaci o dosud nejlepším řešení. Je-li to optimální řešení, pak opět dojde k ukončení výpočtu. Jinak proběhne po vyprázdnění všech zásobníků distribuované ukončení výpočtu pomocí algoritmu "ADUV" (viz. dále) bez nutnosti následné redukce lokálních řešení. V porovnání s lokální strategií vede tato strategie k vyšší komunikační režii, což je patrné z naměřených grafů, ale zase dovoluje eliminovat prohledávání větší časti stavového prostoru, protože každý procesor zná momentálně nejlepší globální řešení a častěji pozná zbytečnost prohledávání v podprostorech. V tomto systému se projeví nastavení tzv. "řezné hladiny", jejiž špatné nastavení může zdržet doručení nového minima a způsobit zbytečné prohledávání již ořezaného podstromu. Z globálního poledu by asi bylo lepší řešit problém prohledáváním do šířky. Prohledávání do hloubky z důvodu výskytu cyklů vede k hledání nejkratšího řešení odzadu postupným zkracováním nejhoršího řešení. Prohledávání do šířky by vedlo nejprve k nalezení řešení nejkratšího a teprve pak k hledání delších řešení, které už by nás ale nezajímaly a algoritmus by se proto mohl ukončit.
Algoritmus pro hledání dárce ACZ-AHD (asynchronní cyklické žádosti):
Každý procesor si udržuje lokální čítač D, kde 1<= D <=p, označující potenciálního dárce. Procesor s prázdným zásobníkem pošle žádost o práci procesoru PD a inkrementuje čítač D mod p. Může se stát, že jeden a tentýž procesor obdrží několik žádostí o práci.
Každý procesor začína s D=(vlastniID+1), aby se nestalo, že všichni začnou žádat na začátku ten stejný procesor. Žádosti o práci jsou obsluhovány sekvenčně a každý žádající dostane polovinu zásobníku dárcova procesoru.
Algoritmus dělby zásobníku R-ADZ (půlení na prahu řezné výšky):
Žadatel obdrží polovinu stavů z výšky H či menší. Pro každou úlohu bylo třeba stanovit práh řezné výšky H, což je maximální výška zásobníku, do které se bude dělení provádět. My jsme zvolili hladinu tak, aby ji byl schopen procesor dosáhnout v rozumně níském čase což je asi přibližně 1x za 5-10s. Experimentálně jsme změřili, že za 5-10s je algoritmus schopen projít stom s průměrnou hloubkou 4-5 a tak jsme i nastavili hladinu H. Hodnoty hladiny uvádime jako součást konfigurace paralelního algoritmu. Tento způsob vyvažování zátěže je pro naše zadání zcela nevhodný. Vede na stálé prohledávání kolem dna stavového prostoru i přesto, že předpokládané řešení je pravděpodobně někde u vrcholu. Také to vede na velkou režii při dělení zásobníku, který má obvykle délky 100-vek prvků a jeho procházení až k řezné hloubce a následné půlení v tomto místě je časově velmi náročné.
Struktura programu:
První proces na začátku provede expanzi prvního stavu zásobníku a expandované stavy rozdělí podle počtu procesorů tak, aby mu samotnému zbyla nějaká práce. Poté všem procesorům pošle inicializační paket, na který ostatní procesy čekají. V něm se dozví velikost práce, kterou v zápětí přijmou. Všechny procesy tedy začnou prohledávat svoji část stavového prostoru. Smyčka aktivity procesoru jde vidět na obrázku:
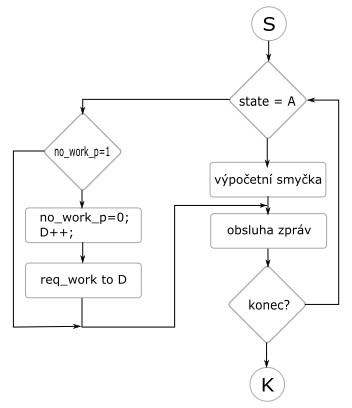
Je vidět, že po odeslání požadavku se již nechodí do výpočetního cyklu, ale jen se zpracovávají zprávy a čeká se na odpověď, případně ukončení výpočtu, a odmítají se požadavky o práci od jiných procesorů.
3 Naměřené výsledky a jejich zhodnocení
Naměřené hodnoty:
| Konfigurace | Ethernet | Myrinet | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 CPU | 2 CPU | 4 CPU | 8 CPU | 12 CPU | 1 CPU | 2 CPU | 4 CPU | 8 CPU | 12 CPU | |
| S=5, N=6, R=4, H=4 | 181s | 291s | 45s | 27s | --s | 181s | 253s | 28s | 27s | --s |
| S=6, N=6, R=1, H=4 | 210s/274s | 197s | 83s | 81s | 68 | 210s/274s | 197s | 84s | 80s | 68s |
| S=7, N=6, R=0, H=4 | 1202s | t>1h | 691s | 1243s | 934s | 1202s | t>1h | 706s | 1286s | 945s |
| 3m úloha | 90s | 48s | 24s | 13s | 10s | 96s | 46s | 24s | -- | -- |
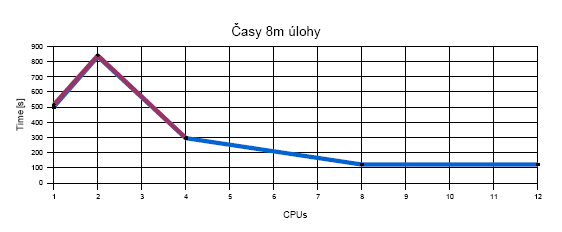
| 8m úloha | 502s | 833s | 296s | 122s | 122s | 516s | 841s | 297s | -- | -- |
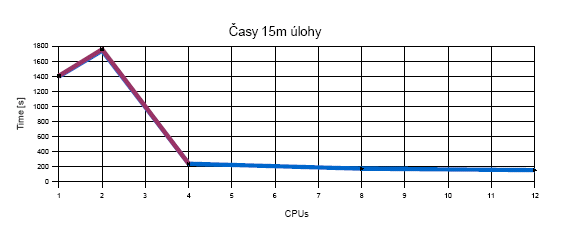
| 15m úloha | 1400s | 1743 | 240s | 173s | 153s | 1410s | 1762s | 240s | -- | -- |
Konfigurace pro poslední 3 úlohy jsou následující:
- 3m úloha : S=6, N=5, R=4, H=6
- 8m úloha : S=6, N=6, R=5, H=6
- 15m úloha : S=6, N=6, R=5, H=6
Výsledné grafy:
Časy výpočtu
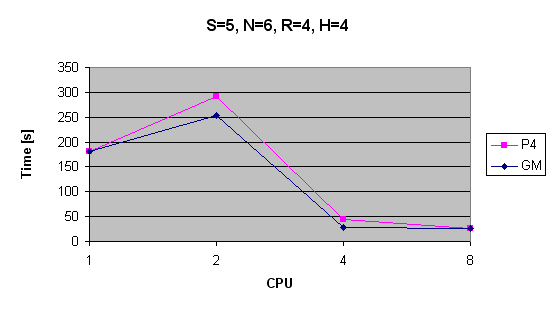
Zrychlení
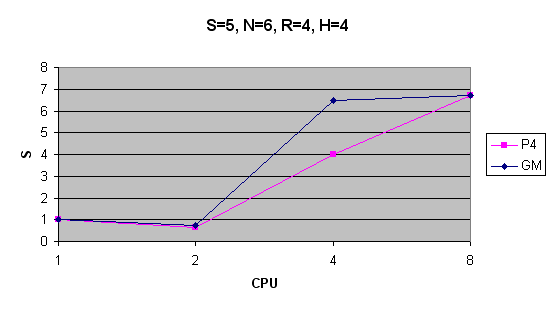
Časy výpočtu
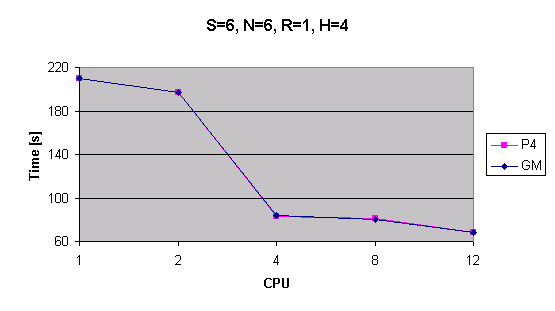
Zrychlení
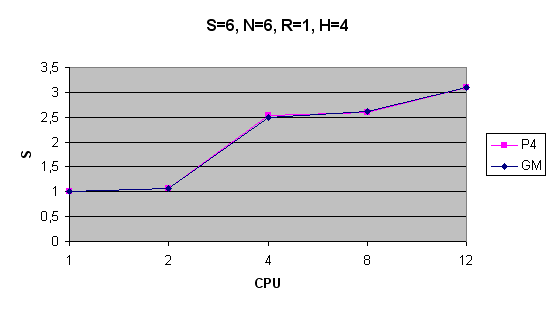
Časy výpočtu
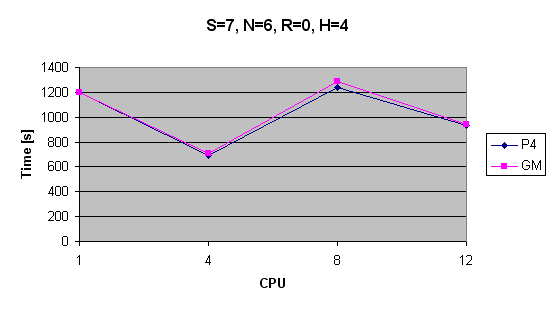
Zrychlení
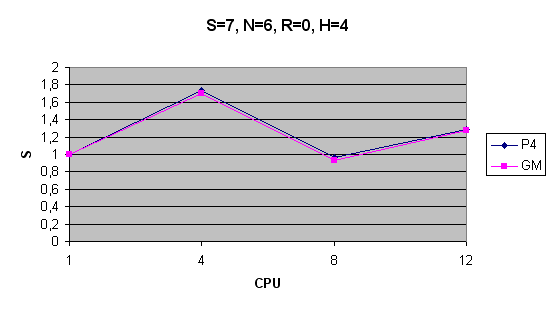
Časy výpočtu:
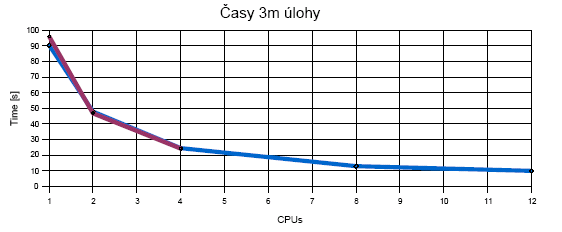
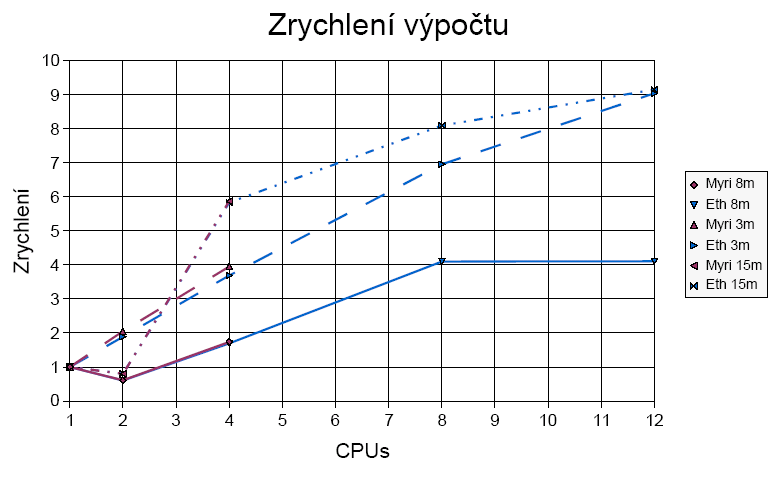
Zrychlení:
Komunikační složitost:
Program prochází několika fázemi. V první fázi se rozděluje práce, ve druhé se provádí výpočet, ve třetí fázi dochází k rozesílání ukončovacích zpráv a v poslední čtvrté se posílají jednotlivé časy uzlu 0 (pro výpočet celkového procesorového času). Fázemi 1, 3 a 4 proces projde jen jednou. Takže zde máme konstantní časovou složitost. Ve fázi 2 dochází k vlastnímu výpočtu. Tento výpočet je pravidelně přerušován a podle vývojového diagramu v odstavci "Struktura programu" dochází k obsluze zpráv (blok "obsluha zpráv"). V obsluze se zjišťuje, jestli čekají nějaké zprávy na přijetí a pokud ano, tak je přijme a zpracuje. Pokud rozdělujeme práci, tak bereme v úvahu hloubku, která je nastavená napevno. V našem případě se pohybuje okolo 5-6 úrovní od listů stromu. Obsahuje práci na pár sekund. Takže pokud dojde práce po úvodním rozdělení, začíná se komunikovat celkem pružně, ale zase ne moc, aby to zbytečně nezpomalovalo výpočet.
Z toho plyne, že by bylo lepší dělit zásobník co nejblíže ke kořeni stromu. Čím jsme blíže kořeni, tím více práce daný podstrom obsahuje a tím méně je potřeba komunikovat.
Co se týče algoritmu na výběr dárce, tak ten rotuje postupně všechny uzly bez ohledu na to, od koho práci dostane a od koho ne. Lze ale předpokládat, že ten, kdo práci měl, tak ji bude mít i příště. Minimálně z toho důvodu, že je úroveň přidělování práce nastavena na nízkou hodnotu. Pokud bude počáteční rozdělení práce rovnoměrné, pak by mělo být vše v pořádku. Pokud ale P0 při inicializaci rozdá jen minimum práce, pak budou všechny požadavky končit u P0, které bude více vytěžováno a hodně bržděno obsluhou požadavků. Navíc se pokaždé musí oběhnout kolečko přes všechny uzly.
Granularita problému
Jak je vidět z grafů, zvýšení počtu procesorů se pozitivně projevuje až při jejich vyšším počtu. Zlepšování času nutného pro výpočet závisí na mnoha aspektech. Proces ve fázi 2 je pravidelně přerušován po určitém počtu cyklů. Z toho plyne maximální doba pro zpoždění při komunikaci mezi procesory. Dále je dána hranice, která určuje množství práce při žádosti. Z toho plyne jednoduchá nerovnice, která nám řekne, kdy už se nevyplatí zvyšovat počet procesorů:
"počet procesorů" * "prům. doba odezvy" < "doba zpracování bloku práce"
Pokud splníme tuto rovnici, pak máme šanci, že přidání dalšího procesoru urychlí výpočet.
Tato úloha také vykazuje silně anomální chování. Při hledání optimální konfigurace pro měření jsem se setkal s případem, kdy nalezení řešení na jednom uzlu trvalo okolo 68 vteřin. Při použití 2 uzlů došlo k ukončení výpočtu za zlomek času: cca 5 vteřin. Je to jasné superlineární zrychlení. Došlo k tomu zásluhou dobře rozděleného stavového prostoru mezi uzly, kde 2. uzel měl řešení takřka "pod nosem".
4 Literatura
- http://star.felk.cvut.cz
- Skripta: Paralelní systémy a algoritmy, Prof. Ing. Pavel Tvrdík, CSc., Leden 2005 vydavatelství ČVUT, ISBN 80-01-02267-6